Introduction
여러 논문들을 보다보면 Manifold라는 단어는 자주 나오지만 이에 대해서 이해하기 어려웠습니다. 그래서 이번글을 통해서 해당 개념을 정리해보겠습니다.
What is “Manifold”
Manifold의 사전적인 의미를 보면 “국소적으로 유클리드 공간과 닮은 위상 공간이다”라고 적혀있습니다. 다르게 말하면 공간의 부분집합들이 국소적으로 유클리드 공간과 닮은 구조를 가지는 공간을 의미합니다.
사전적인 의미로는 수학적인 정의로 되어 있어 이것이 의미하는 바를 직접적으로 이해하기도 힘듭니다.
그래도 먼저 사전적인 의미를 예제로 가볍게 살펴보겠습니다.
“국소적으로 유클리드 공간과 닮아있다.”라는 것에서 유클리드 공간는 흔히 사용하는 공간을 의미하며, 피타고라스 정리로 계산이 가능한 거리개념의 공간이라고 보면 됩니다.
지구 전체를 보면 곡선의 형태인 구이지만, 국소적으로 보면 평면으로 볼 수 있습니다. 즉, 자주 사용하는 구글 지도를 보면 평평한 지도이지만, 실제로는 지구는 구형태를 가지고 있습니다. 지구처럼 형태가 평평하지는 않지만 국소적으로 평평한 공간에 그려낼 수 있는 형체를 다양체(Manifold)라고 부릅니다.
Manifold Hypothesis
Manifold Hypothesis은 실제 세계에서 발생하는 많은 고차원 데이터 세트가 실제로 고차원 공간 내부의 저차원 잠재 Manifold를 따라 놓여 있다고 가정합니다. 즉, 수집한 데이터를 저차원 공간으로 매핑할 수 있다는 것을 의미합니다.
정확히는 sparse 한 고차원 데이터를 간추려서 보다 저차원 공간으로 나타낼수 있다는 뜻입니다.
Manifold를 설명할 때 자주 사용되는 스위스롤예제를 통해서 보겠습니다.
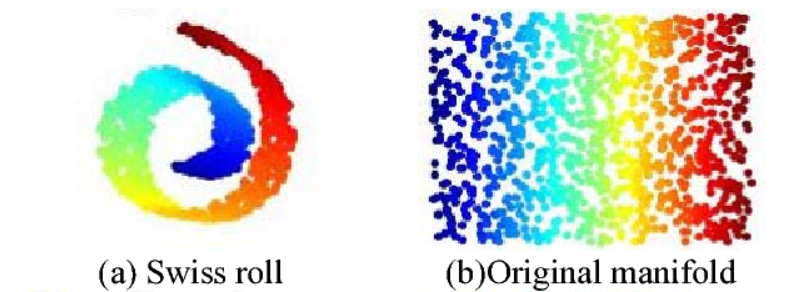
위 그림(a)에서 빨간색부분과 파란색 부분의 유클리드거리(직선거리)는 가깝지만, 실제로는 서로 안 닮은 데이터입니다. 하지만 어떤 데이터간의 닮음을 측정할 때는 보편적으로 유클리드거리를 많이 사용하고, 이런 경우에는 서로 다른 데이터를 닮았다고 할 수 있습니다.
일반적으로 딥러닝에서 Manifold를 학습하는 것은 (b)와 같이 데이터의 특성을 잘 표현하는 공간을 찾는 방법을 말합니다.
Reference
Uploaded by N2T
'AI > Basics' 카테고리의 다른 글
| Maximum Entropy Principle (0) | 2023.07.28 |
|---|---|
| MLE, MAP (0) | 2023.07.28 |
| Mutual Information (0) | 2023.07.24 |
| Probability vs Likelihood (0) | 2023.07.24 |